Exponential growth, doubling time, and the Rule of 70
Exponential growth is growth that occurs at a constant rate, such as an investment that grows at an annual 7 percent rate. The Rule of 70 provides a quick and easy way to determine how long it will take for an amount to double at a given growth rate. Simply divide the percentage number into 70 to obtain the approximate number of years required to double. A more detailed description is given below.
Populations can grow at a constant rate, thus the Rule of 70 can be used to approximate the doubling time of a population that is growing at a fixed rate of growth.
Human population has generally grown in an exponential manner throughout human history, and projections of exponential doubling times have been applicable.
Current dynamics of population growth are more complex and population growth can no longer be considered to be precisely exponential. Population issues of the 21st Century include migration and immigration, aging, Baby Boomers and the youth bulge, as well as continued population growth in developing countries - all of which result in pressure on sustaining resources and the environment.
Many countries will continue to double their population. The United States is projected to double its population this century, practically within the lifetimes of children born today. Therefore it is appropriate to reference the time in which these countries will double their population. Doubling time is perhaps the most illuminating manner of presenting population growth to the lay person. However, it should be noted that the explanations below refer to a constant rate of growth, which as we note, is not as applicable to countries now as it was in the past.
Exponential Growth
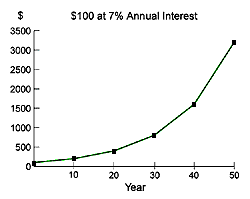
A quantity grows exponentially when its increase is proportional to what is already there. A common example is compound interest, where $100 invested at 7% per year annual compound interest will double in 10 years. Similarly, if a population grows at 7% per year, it, too, will double in 10 years.
Exponential growth has surprising consequences. $100 invested at a 7% annual return will double in 10 years to approximately $200, double in another 10 years to approximately $400, and double again in the next 10 years to approximately $800. Significant gains can be made by simply relying on exponential growth over time. One way of saying this is that the longer you wait on your investment, the faster your returns come in. In the following graph, you can see that over time, returns increase dramatically.
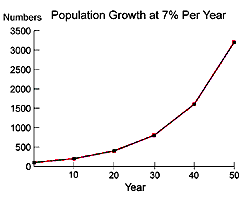
There are also clear disadvantages to exponential growth. When populations continue to grow, the impact of growth becomes increasingly significant over time. Because of the nature of exponential growth, "when things get bad, they get bad in a hurry".
Consider a city with 100,000 people, growing at 7% per year. In 10 years, the population will double to 200,000 people, in another 10 years it will double again to 400,000 people, and ten years after that it will double again to 800,000 people. The following graph shows this exponential population growth. The shape of the curve is identical to the interest rate graph above!
The Rule of 70
The Rule of 70 states that to find the doubling time of a quantity growing at a given annual percentage rate, divide the percentage number into 70 to obtain the approximate number of years required to double. For example, at a 10% annual growth rate, doubling time is 70 / 10 = 7 years.
Similarly, to get the annual growth rate, divide 70 by the doubling time. For example, 70 / 14 years doubling time = 5, or a 5% annual growth rate.
Doubling times
The following table shows some common doubling times:
| Growth Rate (% per year) |
Doubling Time in years |
| 0.1 | 700 |
| 0.5 | 140 |
| 1 | 70 |
| 2 | 35 |
| 3 | 23 |
| 4 | 18 |
| 5 | 14 |
| 6 | 12 |
| 7 | 10 |
| 10 | 7 |
Understanding Exponential Growth
See this interesting interactive tutorial on Understanding Exponential Growth.
The Math Behind the Rule of 70
From Dick Schneider, Californians for Population Stabilization:
The use of natural logs arises from integrating the basic differential equation for exponential growth: dN/dt = rN, over the period from t=0 to t = the time period in question, where N is the quantity growing and r is the growth rate.
The integral of that equation is:
N(t) = N(0) x ert
where N(t) is the size of a quantity after t intervals have elapsed, N(0) is the initial value of the quantity, e is the base of the natural logarithm, r is the average growth rate over the interval in question, and t is the number of intervals. Natural logarithms (that is, logarithms to the base e) come in from this integration. Natural logs are sometimes abbreviated ln to distinguish them from "common" logarithms of base 10.
In our case, t is usually given in years and r is the average annual growth rate. However, the formula works for seconds, weeks, centuries, etc.
The ratio of the final to the initial values of N is N(t)/N(0), and is equal to ert power. (Dividing through by N(0).)
The natural logarithm of the ratio N(t)/N(0) is equal to rt. (Taking the natural log of e raised to a power is simply the power itself.)
The growth rate r is then given by natural log N(t)/N(0) divided by t.
Alternatively, if one knows the final and initial values of N and the average growth rate, one can find the time it takes at that average growth rate for the quantity to grow from its initial value to the final value.
t = ln [ N(t)/N(0) ] / r
A special case is the doubling time, which is the time when N(t)/N(0) = 2, that is the quantity has doubled from its initial value. At that point
rt = ln 2 = 0.69
If one knows the growth rate as a decimal fraction, then the doubling time t2 = 0.69 / r.
If the growth rate is given in percent, then 0.69 must be multiplied by 100, and the doubling time = 69/r. This is the origin of the rule of 70, i.e., 69 is rounded up to 70.
For the results to be accurate, all of these calculations assume that the growth rate remains unchanged throughout the interval in question, that is, that the growth is exponential at the average rate for the entire period. Most quantities don't really grow that way (compound interest is an exception), so this method is generally an approximation for the real world.
When considering growth over a period of years, it is important to note that taking the natural logarithm of the ratio of the final value to the initial value and dividing by the time period in years gives the average annual growth rate.
For example, metro Denver population grew 15% from 1990 to 1996. The simple arithmetic average of growth is 2.5% per year (15% / 6 years = 2.5%/year). Strictly speaking the rule of 70 applies to exponential growth, which means that the compound average population growth rate must be divided into 70 to get the doubling time.
The compound average growth rate involves natural logarithms. To find the compound growth rate, take the natural log of the ratio of the final to the initial populations and divide this by 6 years. 15% growth means that the ratio of final to initial populations is 1.15. (The final population is 115% of the initial population, considered to be 100%; 115% / 100% = 1.15.) The natural log of 1.15 is 0.14. Dividing 0.14 by 6 years = 0.023/year, or an average geometric increase of 2.3% / year.
Finally, divide 70 by 2.3 to give a doubling time of 30 years.